Introdução ao GAM

O que são GAMs?

GAM significa Modelos de Adição Generalizados (Generalized Additive Models). Está técnica é utilizada em estatística, quando se deseja utilizar funções suaves para as variáveis de predição e suas interações. De modo simplificado, as funções suaves obtidas através de várias funções cúbicas (na prática, funções mais complexas são utilizadas).

Quando eu devo utilizar GAMs?

É recomendado utilizar GAMs quando a forma da função de predição é desconhecida mas as variáveis de predição são conhecidas. Por exemplo, poderíamos estimar a temperatura ao longo do dia. Neste exemplo, usaríamos a temperatura como variável predita e a hora do dia como variável de predição.

Exemplo: Predição da variação da temperatura ao longo do dia

Vamos explorar um exemplo artificial em que desejemos predizer a temperatura ao longo do dia. Vamos criar nosso conjunto de dados

# criando o horário de 0 a 24 h com 1000 amostras
hora = seq(0, 24, length.out = 1e3)
# criando a temperatura como um valor fixo de 25 graus mais uma oscilação de 5 graus
temp_real = 25 + 5*sin(hora/24*2*pi)

plot(hora, # x
     temp_real, # y
     type = 'l', # plot linha
     xlab = "Hora do dia", # nome do eixo x
     ylab = expression(paste("Temperatura ("^{o},"C)", sep = "")), # nome do eixo y 
     ylim = c(18, 32), # limites do eixo y
     lwd = 10, # espessura da linha
     lty = 2, # tipo da linha
     xaxs = "i", # o eixo x inicia-se no limite inferior de x e termina no limite superior de x
     yaxs = "i", # o eixo y inicia-se no limite inferior de y e termina no limite superior de y
     mgp=c(2.3,0.7,0), # aumenta a posição dos textos dos eixos
     cex.lab = 1.4, # aumenta o tamanho do texto dos eixos
     cex.axis = 1.4) # aumenta o tamanho dos textos dos números dos eixos
grid() # cria linhas guias

# vamos agora adicionar um ruído nesta medida
set.seed(1) # definindo a seed para podermos repetir essa simulação
erros_medida = rnorm(length(hora))
temp_medida = temp_real + erros_medida

lines(hora, # x
      temp_medida, # y
      col = 'red', # cor
      lwd = 4) # espessura da linha

# plotando a real novamente para que ela fique por cima da temperatura medida
lines(hora, # x
      temp_real, # y
      lwd = 10, # espessura da linha
      lty = 2) # tipo da linha

# criando uma legenda
legend('topright', # posição da legenda
       c("Real", "Medida"), # texto na legenda
       lwd = 7, # espessura das linhas na legenda
       lty = c(2, 1), # tipos da linha na legenda
       col = c('black', 'red'), # cores das linhas na legenda
       cex = 2) # aumenta o tamanho da legenda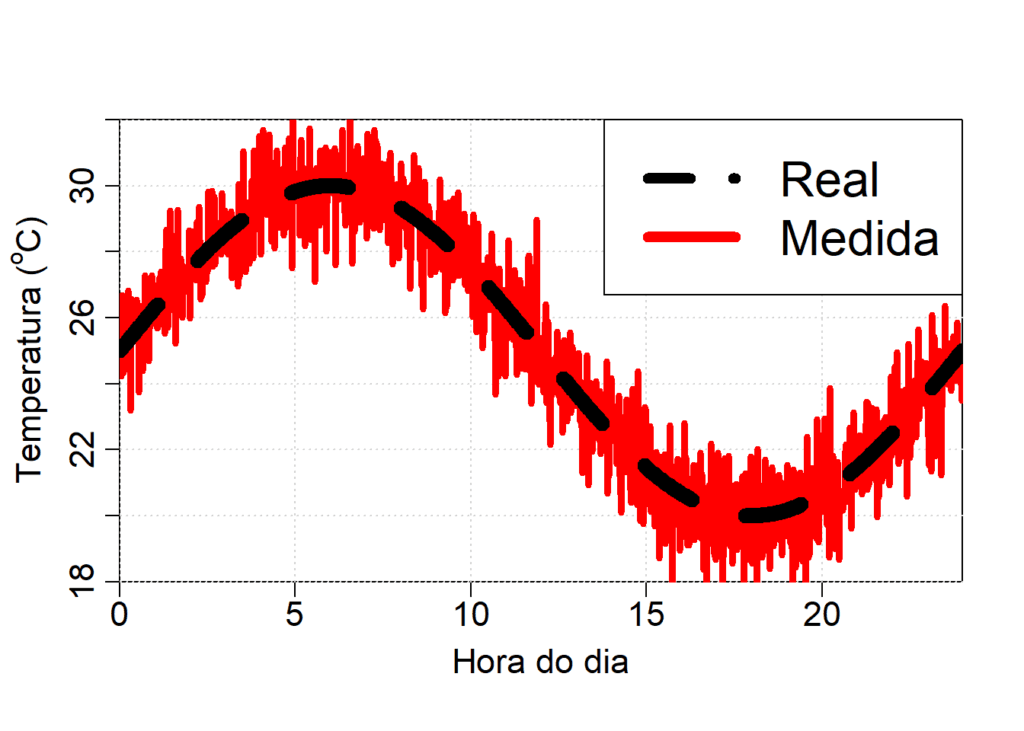

Agora que temos o conjunto de dados criado, podemos treinar nosso modelo GAM. Para isso, vamos precisar das bibliotecas do R chamadas de mgcv e nlme.

library(mgcv) # iniciando a biblioteca mgcv que também inicia a biblioteca nlme

## Loading required package: nlme
## This is mgcv 1.8-31. For overview type 'help("mgcv-package")'.

# treinando o modelo GAM
model.gam = gam(temp_medida # o que queremos predizer
                ~ # a fórmula de predição depois do ~ 
                  s(hora) # s(.) define uma função suave da hora
                )
# agora olhas no sumário do modelo.
# Vemos que o modelo conseguiu explicar 92.3% dos desvios
summary(model.gam)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## temp_medida ~ s(hora)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 24.98835    0.03277   762.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##           edf Ref.df    F p-value    
## s(hora) 7.049  8.112 1451  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.922   Deviance explained = 92.3%
## GCV = 1.0827  Scale est. = 1.074     n = 1000

# agora vamos plotar o modelo e comparar com a função real.
# obtendo a temperatura estimada
temp_estimada = predict(model.gam, data.frame(hora = hora))

# vamos plotar as mesmas coisas que antes
plot(hora, # x
     temp_real, # y
     type = 'l', # plot linha
     xlab = "Hora do dia", # nome do eixo x
     ylab = expression(paste("Temperatura ("^{o},"C)", sep = "")), # nome do eixo y 
     ylim = c(18, 32), # limites do eixo y
     lwd = 10, # espessura da linha
     lty = 2, # tipo da linha
     xaxs = "i", # o eixo x inicia-se no limite inferior de x e termina no limite superior de x
     yaxs = "i", # o eixo y inicia-se no limite inferior de y e termina no limite superior de y
     mgp=c(2.3,0.7,0), # aumenta a posição dos textos dos eixos
     cex.lab = 1.4, # aumenta o tamanho do texto dos eixos
     cex.axis = 1.4) # aumenta o tamanho dos textos dos números dos eixos
grid() # cria linhas guias

lines(hora, # x
      temp_medida, # y
      col = 'red', # cor
      lwd = 4) # espessura da linha

# plotando a real novamente para que ela fique por cima da temperatura medida
lines(hora, # x
      temp_real, # y
      lwd = 10, # espessura da linha
      lty = 2) # tipo da linha

lines(hora, # x
      temp_estimada, # y
      lwd = 10, # espessura da linha
      lty = 3, # tipo da linha
      col = 'gold')

# criando uma legenda
legend('topright', # posição da legenda
       c("Real", "Medida", "Estimada"), # texto na legenda
       lwd = 7, # espessura das linhas na legenda
       lty = c(2, 1), # tipos da linha na legenda
       col = c('black', 'red', 'gold'), # cores das linhas na legenda
       cex = 2) # aumenta o tamanho da legenda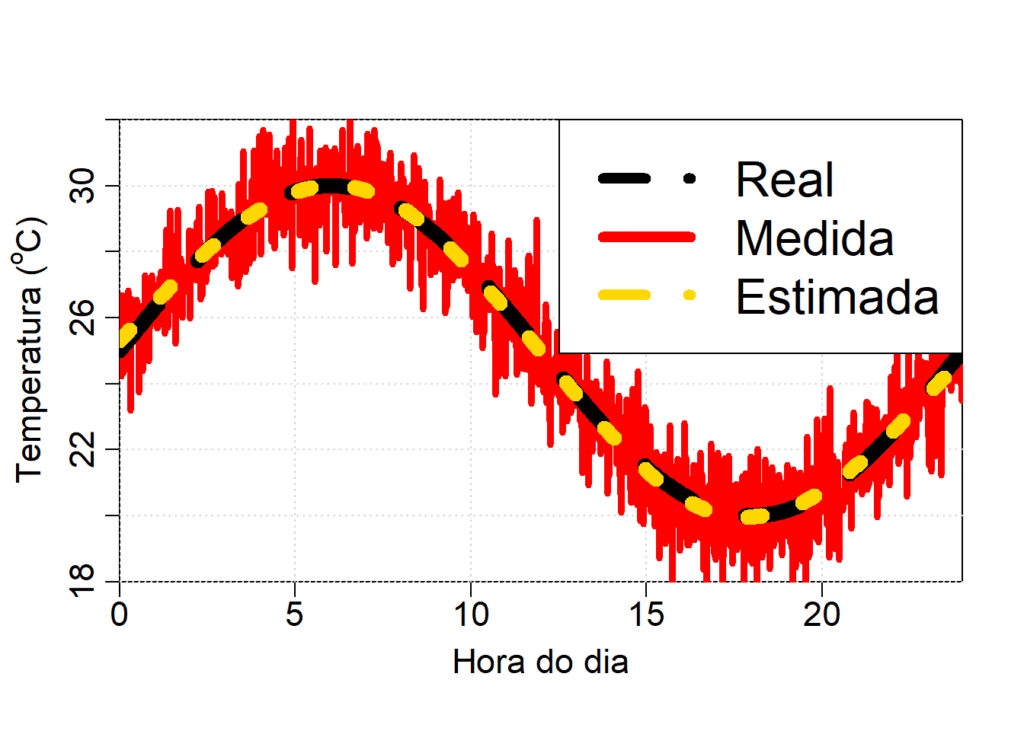

Como podemos ver na figura acima, a temperatura estimada com o modelo GAM é muito similar a temperatura real.

#  vamos plotar a diferença
plot(hora, # x
     temp_real - temp_estimada, # y
     type = 'l', # plot linha
     xlab = "Hora do dia", # nome do eixo x
     ylab = expression(paste("Erro da temperatura estimada("^{o},"C)", sep = "")), # nome do eixo y 
     ylim = c(-0.3, 0.3), # limites do eixo y
     lwd = 10, # espessura da linha
     lty = 2, # tipo da linha
     xaxs = "i", # o eixo x inicia-se no limite inferior de x e termina no limite superior de x
     yaxs = "i", # o eixo y inicia-se no limite inferior de y e termina no limite superior de y
     mgp=c(2.3,0.7,0), # aumenta a posição dos textos dos eixos
     cex.lab = 1.4, # aumenta o tamanho do texto dos eixos
     cex.axis = 1.4) # aumenta o tamanho dos textos dos números dos eixos
grid() # cria linhas guias

# eu gosto de replotar a linha para colocar a linha acima das linhas de grade:
lines(hora, # x
      temp_real - temp_estimada, # y
      lwd = 10, # espessura da linha
      lty = 2) # tipo da linha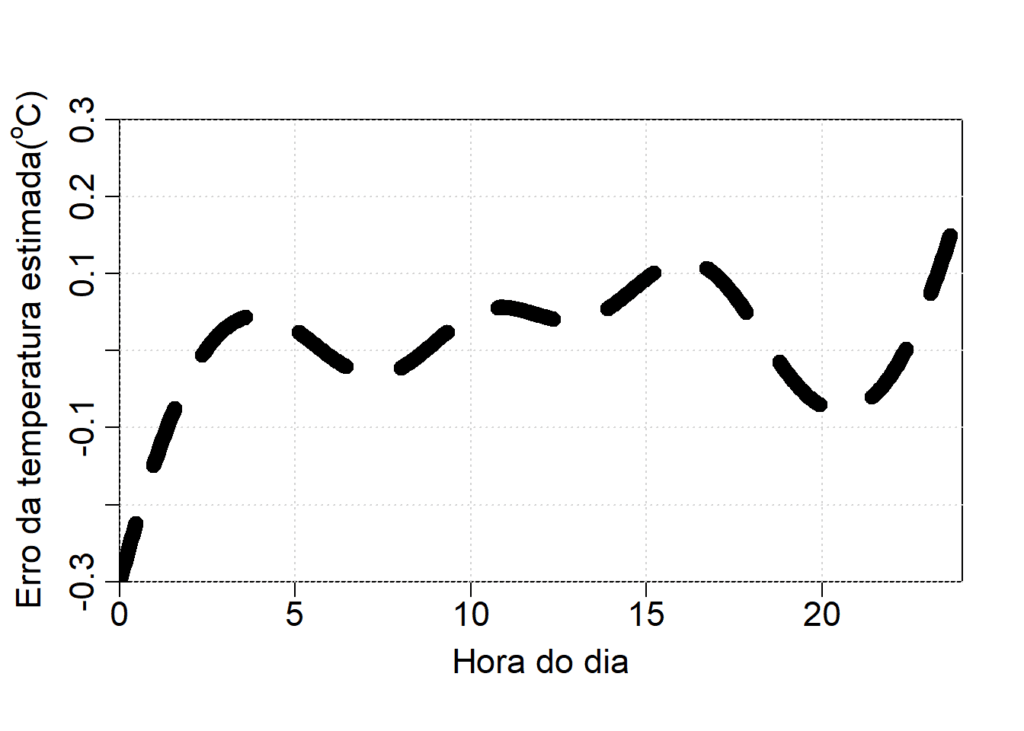

Onde posso ir para aprender mais?

A literatura recomendada é a seguinte:

• Livro que introduz diversas técnicas estatísticas no ambiente R. Zuur AF, Ieno EN, Walker NJ, Saveliev AA, Smith GM. Mixed Effects Models and Extensions in Ecology with R. Springer, New York, 2009.
• Livro que descreve a teoria de GAMs utilizando o ambiente R. Wood SN. Generalized Additive Models: An Introduction with R (2nd ed.). CRC Press, Boca Raton, 2017.
• Livro que descreve vários métodos de aprendizado de máquina. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer, New York. 2008.
• Livro que descreve vários métodos de aprendizado de máquina. Efron B, Hastie T. Computer Age Statistica Inference: Algorithms, Evidence, and Data Science. Cambridge University Press, Cambridge, 2016.